Approximating $\pi$ with polygons
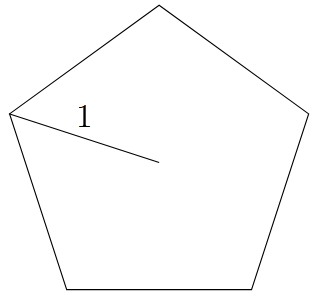
The radius of a regular polygon is the distance from the center of the polygon to any one of its vertices. Let $P_n$ be a regular polygon with $n$ sides and radius $1$. The pentagon $P_5$ is shown below:
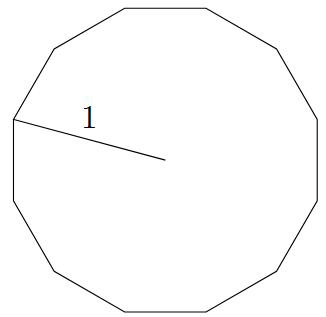
As we increase $n$, the polygon looks more and more like a circle. Here is $P_{12}$:
Let $A_n$ be the area of $P_n$. Then the limit of $A_n$ as $n\to\infty$ is actually $\pi$, the area of a circle with radius $1$. One way to convince ourselves of this fact is by bounding $P_n$ with an outer circle and an inner circle.
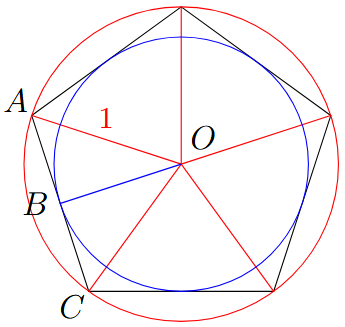
The outer circle has radius $1$ as labelled in the diagram. The inner circle’s radius (i.e. the length of line segment $\overline{OB}$) is not as obvious. Notice that the polygon consists of $n$ copies of the triangle $OAC$ (one copy per side). The sum of the central angles is $n\angle AOC = 2\pi$, so $\angle AOC = \frac{2\pi}{n}$. Now note that $\angle ABO = \frac{\pi}{2}$ since the line segment $\overline{AC}$ is tangent to the blue circle at $B$. Hence, triangles $OAB$ and $OCB$ are congruent by the Hypotenuse-Leg rule, so $\angle AOB = \angle COB$. Since $\angle AOB + \angle COB = \angle AOC = \frac{2\pi}{n}$, it follows that $\angle AOB = \frac{\pi}{n}$. Therefore, the radius of the inner circle is $\cos(\frac{\pi}{n})$.
Taking the areas of the bounding circles yields the inequality $\pi\cos^2(\frac{\pi}{n})\leq A_n\leq \pi(1^2) = \pi$. Since $\lim_{n\to\infty} \pi\cos^2(\frac{\pi}{n}) = \pi\cos^2(0) = \pi$, the Squeeze Theorem implies that $\lim_{n\to\infty} A_n = \pi$. We will use this observation to obtain an algorithm for approximating $\pi$.
First, let’s obtain a formula for $A_n$. Observe that triangle $OAC$ in the previous diagram has base length $2\sin(\frac{\pi}{n})$ and height $\cos(\frac{\pi}{n})$, so its area is $\sin(\frac{\pi}{n})\cos(\frac{\pi}{n})$. Since $P_n$ consists of $n$ copies of $OAC$, we see that $A_n = n\sin(\frac{\pi}{n})\cos(\frac{\pi}{n}) = \frac{1}{2}n\sin(\frac{2\pi}{n})$. However, this formula for $A_n$ depends on $\pi$, and using $\pi$ to approximate $\pi$ is circular. How can we eliminate the dependency on $\pi$?
The trick is to consider $x_n = A_{2^n} = 2^{n-1}\sin(\frac{\pi}{2^{n-1}})$ for $n\geq 2$. We have that $\lim_{n\to\infty} x_n = \lim_{n\to\infty} A_{2^n} = \pi$ because the indices $2^n$ go to $\infty$ as $n\to\infty$. However, note that that the argument to the sine function is halved each time we increase $n$ by $1$. Perhaps we could use a double-angle formula such as $\cos(2\theta) = 2\cos^2(\theta) - 1$ to obtain a recursive formula for $x_{n+1}$ in terms of $x_n$, without any dependence on $\pi$. Here are the three basic double-angle formulas that I know:
\[\sin(2\theta) = 2\sin(\theta)\cos(\theta)\] \[\cos(2\theta) = 2\cos^2(\theta) - 1\] \[\cos(2\theta) = 1 - 2\sin^2(\theta)\]We have a problem: each of these formulas depends on cosine, and our formula for $x_n$ doesn’t have cosine in it. Fortunately, there is a simple fix: we can use the Pythagorean identity
\[\sin^2\left(\frac{\pi}{2^{n-1}}\right) + \cos^2\left(\frac{\pi}{2^{n-1}}\right) = 1\]to write
\[x_n = 2^{n-1}\sqrt{1 - \cos^2\left(\frac{\pi}{2^{n-1}}\right)}.\](Note: we use the positive square root because $\frac{\pi}{2^{n-1}}\in (0, \frac{\pi}{2}]$ for all $n\geq 2$, which means $\sin(\frac{\pi}{2^{n-1}}) > 0$ for all $n\geq 2$.)
Now we can use the formula $\cos(2\theta) = 2\cos^2(\theta) - 1$ to write $x_{n+1}$ in terms of $x_n$. Let’s do some algebra:
\[\begin{align*} &x_{n+1} = 2^n\sqrt{1 - \cos^2\left(\frac{\pi}{2^n}\right)} \\ \implies &\frac{x_{n+1}^2}{2^{2n}} = 1 - \cos^2\left(\frac{\pi}{2^n}\right) \\ \implies &\cos^2\left(\frac{\pi}{2^n}\right) = 1 - \frac{x_{n+1}^2}{2^{2n}} \\ \implies &2\cos^2\left(\frac{\pi}{2^n}\right) - 1 = 2\left(1 - \frac{x_{n+1}^2}{2^{2n}}\right) - 1 = 1 - \frac{x_{n+1}^2}{2^{2n-1}} \\ \implies &\cos\left(\frac{\pi}{2^{n-1}}\right) = 1 - \frac{x_{n+1}^2}{2^{2n-1}}\quad\text{(since $2\cos^2(\theta) - 1 = \cos(2\theta)$)} \\ \implies &\left(\frac{x_n}{2^{n-1}}\right)^2 = 1 - \cos^2\left(\frac{\pi}{2^{n-1}}\right) = 1 - \left(1 - \frac{x_{n+1}^2}{2^{2n-1}}\right)^2 \\ \implies &\left(1 - \frac{x_{n+1}^2}{2^{2n-1}}\right)^2 = 1 - \frac{x_n^2}{2^{2n-2}}. \end{align*}\]We know that
\[1 - \frac{x_{n+1}^2}{2^{2n-1}} = \cos\left(\frac{\pi}{2^{n-1}}\right)\geq 0\]since $\frac{\pi}{2^{n-1}}\in [0, \frac{\pi}{2}]$ for all $n\geq 2$. Hence,
\[1 - \frac{x_{n+1}^2}{2^{2n-1}} = \sqrt{1 - \frac{x_n^2}{2^{2n-2}}}.\]Finally, solving for $x_{n+1}$ gives us
\[x_{n+1} = 2^{n - 1/2}\sqrt{1 - \sqrt{1 - \frac{x_n^2}{2^{2n-2}}}}\](and again, we use the positive square root since $x_n > 0$ for all $n$). Multiplying the right-hand side by $\frac{2^{(n-1)/2}}{2^{(n-1)/2}}$ yields the simpler formula
\[x_{n+1} = 2^{n/2}\sqrt{2^{n-1} - \sqrt{2^{2n-2} - x_n^2}}.\]This recursive formula allows us to compute $x_{n+1}$ using only $x_n$ and basic algebraic operations. To fully specify the recurrence, we need the base case $x_2$, which we now directly compute:
\[x_2 = 2^{2-1}\sin\left(\frac{\pi}{2^{2-1}}\right) = 2\sin\left(\frac{\pi}{2}\right) = 2.\]The convergence analysis of this approximation algorithm is quite straightforward. Recall that
\[x_n = 2^{n-1}\sin\left(\frac{\pi}{2^{n-1}}\right).\]Using the Taylor series $\sin(x) = x - \frac{x^3}{3!} + O(x^5)$ gives
\[\begin{align*} x_n &= 2^{n-1}\left[\left(\frac{\pi}{2^{n-1}}\right) - \frac{\pi^3}{6(2^{3n-3})} + O\left(\frac{\pi^5}{2^{5n-5}}\right)\right] \\ &= \pi - \frac{2\pi^3}{3}4^{-n} + O(16^{-n}) \end{align*}\]since constants are ignored in big-O notation. Let’s state our results as a theorem.
Theorem. The recurrence relation
\[\begin{align*} x_2 &= 2, \\ x_{n+1} &= 2^{n/2}\sqrt{2^{n-1} - \sqrt{2^{2n-2} - x_n^2}}\quad\text{for $n\geq 2$} \end{align*}\]satisfies the asymptotic bound $|\pi - x_n| = \frac{2\pi^3}{3}4^{-n} + O(16^{-n})$. In particular, $\lim_{n\to\infty} x_n = \pi$.
Remark. Numerically, I have found the above recurrence to be problematic. For even modest values of $n$ (e.g. $n = 40$), my computer evaluates $2^{n-1} - \sqrt{2^{2n-2} - x_n^2}$ as $0$, which means it evaluates $x_{n+1}$ as $0$. If we square both sides of the recurrence and multiply both sides by $2^{n-1} + \sqrt{2^{2n-2} - x_n^2}$, we can obtain the equivalent formula
\[x_{n+1}^2 = \frac{2^nx_n^2}{2^{n-1} + \sqrt{2^{2n-2} - x_n^2}}\]which I find to work better. Here is a Python script implementing the above recurrence:
import math
squared_xn = 4
for n in range(2, 40):
power = 2 ** (n - 1)
squared_xn = (2 * power * squared_xn) / (power + math.sqrt(power * power - squared_xn))
print(f'|pi - x_{{{n + 1}}}| = {abs(math.pi - math.sqrt(squared_xn))}')
The result:
|pi - x_{3}| = 0.3131655288436028
|pi - x_{4}| = 0.08012519466907486
|pi - x_{5}| = 0.020147501331740703
|pi - x_{6}| = 0.0050441630438538
|pi - x_{7}| = 0.0012614966350401602
|pi - x_{8}| = 0.0003154026570202362
|pi - x_{9}| = 7.885244549177273e-05
|pi - x_{10}| = 1.971322270177822e-05
|pi - x_{11}| = 4.9283126335453176e-06
|pi - x_{12}| = 1.2320785933717104e-06
|pi - x_{13}| = 3.080196755433917e-07
|pi - x_{14}| = 7.700492066220477e-08
|pi - x_{15}| = 1.9251230387595797e-08
|pi - x_{16}| = 4.812807485876647e-09
|pi - x_{17}| = 1.2032019824914642e-09
|pi - x_{18}| = 3.008002735782611e-10
|pi - x_{19}| = 7.52002904391702e-11
|pi - x_{20}| = 1.880007260979255e-11
|pi - x_{21}| = 4.699796107843213e-12
|pi - x_{22}| = 1.1750600492632657e-12
|pi - x_{23}| = 2.935429677108914e-13
|pi - x_{24}| = 7.283063041541027e-14
|pi - x_{25}| = 1.7763568394002505e-14
|pi - x_{26}| = 3.9968028886505635e-15
|pi - x_{27}| = 4.440892098500626e-16
|pi - x_{28}| = 4.440892098500626e-16
|pi - x_{29}| = 4.440892098500626e-16
|pi - x_{30}| = 4.440892098500626e-16
|pi - x_{31}| = 4.440892098500626e-16
|pi - x_{32}| = 4.440892098500626e-16
|pi - x_{33}| = 4.440892098500626e-16
|pi - x_{34}| = 4.440892098500626e-16
|pi - x_{35}| = 4.440892098500626e-16
|pi - x_{36}| = 4.440892098500626e-16
|pi - x_{37}| = 4.440892098500626e-16
|pi - x_{38}| = 4.440892098500626e-16
|pi - x_{39}| = 4.440892098500626e-16
|pi - x_{40}| = 4.440892098500626e-16
As we can see, this implementation is stable and quickly converges to $\pi$. The error terms $|\pi - x_n|$ appear to converge to $2\epsilon$ where $\epsilon = 2^{-52}$ is the machine-epsilon value in Python—but I do not know why.